题目：Regularity of weak solutions and the number of singular points to the 3D simplified nematic liquid crystal system
摘要：In this discussion, I intend to introduce the result of Qiao Liu,who investigate the regularity of weak solutions to the Cauchy problem of 3D simplified nematic liquid crystal flows with the pressure 
bounded from below, or the quanitity of 
is controlled, then we get the globally smooth solution of the nematic liquid crystal system. In addition, he also studies the singular points of weak solutions, if a weak solution satisfies
, with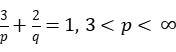 
, then the number of singular points is finite.
参考文献：
[1]G. Seregin, On the number of singular points of weak solutions to the Navier–Stokes equations, Comm. Pure Appl. Math. LIV (2001) 1019–1028.
[2]G. Seregin, V. ˘Sverák, Navier–Stokes equations with lower bounds on the pressure, Arch. Ration. Mech. Anal. 163 (2002) 65–86.
[3]F. Lin, C. Liu, Partial regularities of the nonlinear dissipative systems modeling the flow of liquid crystals, Discrete Contin. Dyn. Syst. Ser. A 2 (1996) 1–23.
时间：2020年7月17日 10:00-11:00
地点：腾讯会议（792764601）
主讲人：吴家彦
人物简介：吴家彦，现为浙江大学博士生，研究方向流体力学，偏微分方程，分数次Laplace方程。